How to map Equirectangular projection to Rectilinear projection
by Nitish S. Mutha
What is Equirectangular Projection?
The projection obtained by a sphere mesh un-wraped on a flat rectangular plane surface is known as equirectangular projection of the sphere (Weisstein [9]). It is the direct mapping of the sphere latitude and longitude on the horizontal and vertical coordinate system respectively. It is also called as “non-projection” or “rectangular projection” as no scaling or transformation are applied. The resulting frame obtained by equirectangular projection appears to be distorted. The objects at the center are spatially compressed and towards the top and bottom are stretched as seen in the figure below Top and bottom regions represents zenith and nadir respectively. Equirectangular frame is of the ratio 2:1. It covers 360° horizontally and 180° vertically. The standard resolution is of the dimension 4096x2048 for UHD resolution.
What is Rectilinear (Gnomonic) Projection?
Rectilinear projection displays the image just like an what an human percieves the world as (undistorted). It has a restricted fiew of view, approximately 114°. Straight lines stay straight, hence making it undistorted.
How to obtain Gnomonic Projection?
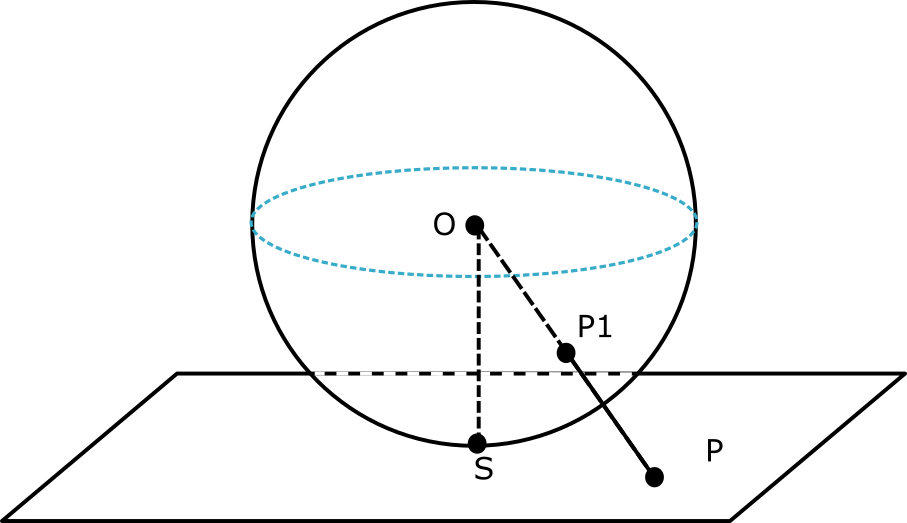
The Gnomonic projection is a map projection which can be achieved by projecting the ray of light from center of the sphere through the surface of the sphere at point P1, which touches on a plane at point P. where the plane is tangent to the sphere at point S as shown in the figure below. This mapping of point from P1 to P on the surface is called Gnomonic map projection.
At the tangent point there is zero distortion, but it increase as we go away from it. It projects great circles on straight lines. It can project a hemisphere of the sphere on the plane.
The Gnomonic projections are used for extracting a NFoV from an equirectangular image. Since an equirectangular image is an unwrapped version of the sphere, the definition and mathematics of Gnomonic projection states the same.
Graphical illustration of the mapping equirectangular/spherical image on to rectilinear image:
Mathematics for plane transformation equations
Let us consider the point S in the Figure above to have the central latitude and central longitude of (lambda_0;phi_1) = (0; 0) which is on the equator and also the center of the plane.
The transformation equations of the plane coordinates are given by,
where c is angular distance of point (x;y) from the center of the projection given as,
While the inverse equations to map the point (x;y) in plane to the sphere are,
Code for the projection mapping
The complete code for mapping eqirectangular to gnomonic/rectilinear projection can be found at https://github.com/NitishMutha/equirectangular-toolbox.
Features of the toolbox
- A tool to extract a normal field of view of any given center point from any given equirectangular image/frame.
- Highly optimized implementation to compute every pixel projection mapping at once, with bilinear interpolation for smoother image.
Code Requirements
- Python 3.5
- Numpy
Subscribe via RSS